we have explain erlier (Law of Resistance) that resistance of the conductor dipending on temprature. so that, here we will show you the effect of rise in temperature:
1) to increase the resistance of pure metal. The increase is large and fairy regular for normal ranges of temperature. The temperature/resistance graph is a straght line (figure 1).
2) to increase the resisrance of alloys, though, in their case, the increase is relatively small and irregular. for some high-resistance alloys like eureka (60% Cu and 40% Ni) and manganin, the increase in resistance is negligible ove a considerable range of temperature.
3) to decrease the resistance of electrolytes, insulators (such as paper, rubber, glass, mica, etc.) and partial conductors such as carbon. hence, insulators are said to prossess a negative temperature-coefisient of resistance.
figure 1 (The temperature/resistance graph)
Temperature-Coefficient of ResistanceLet metallic conductor having aresitance of R0 at 00C be heated to t0C and let ist resistance at this temperature be Rt. then considering normal ranges of temperature, it is found that the increase in resistance:
depends:
1) directly on its initial resistance
2) directly on the rise in temperature
3) on the nature of the material of the conductor
or :
where α (alpha) is a constant and is known as the temperature coeffisient of resistance of that conductor.
rearranging equalition above we get:
If R0 = 1 ohm, t = 1 t0C, the α = Rt – R0
the increase in resistance per ohm original resistance per 0C rise in temperature.
from equation above we find that:
It should be remember the above equation holds good for both rise and fall in temperature as temperature of conductor is decrease, its persistance also decreased in figure below.
figure 2
Figure 2 shown the temperature/resistance graph for copper and is practically a straight line. if this line is extend backward, it would cut the temperature axis at a point where temperature is -234.5 0C, a number quite easy to remember. it means that theoretically, the resistance of copper conductor will become zero at this point though as shown by solid line, in practice, the curve departs from a straight line at very low temperatures. from the two similar triangles of figure 2 it seen that:where α = 1/234.5 for copper


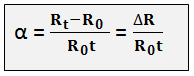





Komentar
Posting Komentar